4. Transformer for Forward converter: Calculation example.

Required Data:
output power: 600W
Vo output voltage: 30 V
I output current: 20 A
Grid voltage VR: 220 Vac +- 20%
Grid frequency fr: 50Hz
Switching frequency f: 100KHz
1. From the known data , through the Table 1 in ETD49 – N67 we find the ferrite suitable for the realization of the transformer. From the catalog we obtain the magnetic properties below. For more information see the catalog in appendix. (AL = 3700nH +30 /-20%).

2. The Table 2 identifies that the maximum allowable overtemperature for the ferrites made with materials N67 is 40 ° C.
3. Table 3 identifies the value of the thermal resistance of the transformer for the ETD49 in 8 °C/W.
4. The maximum power dissipation for the losses in the ferrite and copper in the windings is calculated with (0.2)

5. Calculation of the minimum input DC voltage value (0.3)
Known Data:
Grid voltage: Vr = 220V +-20% VAC
Grid Frequency: fr = 50Hz
Max Peak Voltage: VRi max = (220 + 220*20/100) *SQRT(2) = 373V
Min Peak Voltage: VRi min = (220 – 220*20/100) *SQRT(2) = 249V
Estimated Data:
Efficiency coeffcient 0.8
Input Power : Pi = 600W/0.8 = 750W
Value of Input Capacitor: Ci= 1000uF
Determination of the minimum input voltage:

6. Distribution of power loss (0.5)

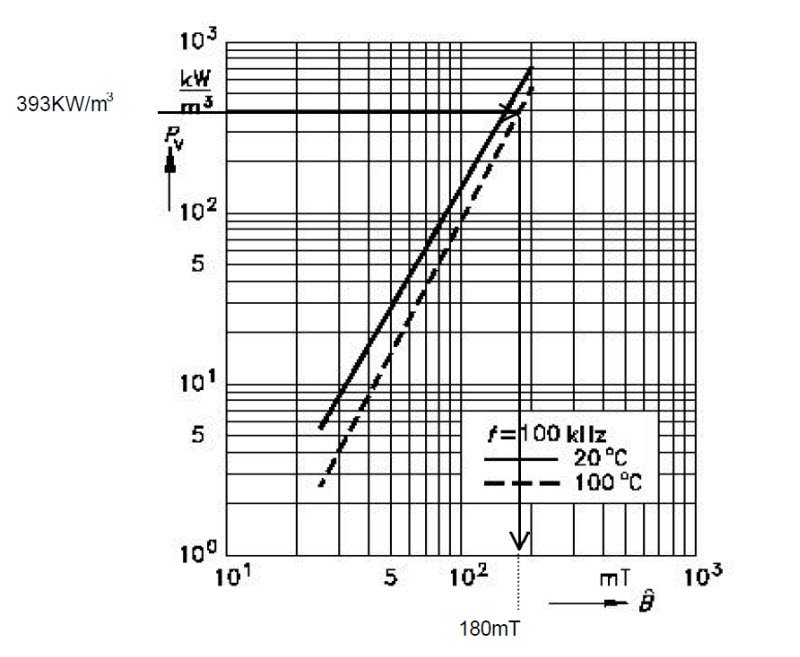
7. Calculation of power lost in specific volume for the ferrite ETD49 (0.6).
Known data:
Power loss in square wave:

Losses single-ended vs push-pull

Considering that the volume of a couple of ferrites ETD49 is 24100 mm^3 , the loss of specific power per unit volume will be:

From the diagram below, for the material chosen N67 Pv = f (f) for f = 100KHz and T = 100 °C we get delta Bmax about 180mT.
8. Determination of the maximum permitted flux delta Bmax as a function of the losses in the ferrite.
9. Calculation of the number of turns in the primary (0.8) and (0.9).
The maximum duty cycle is lower than 0.5 to allow the complete demagnetization of the core


10. Estimation of the resistance in Ohm of the primary winding (0.10)
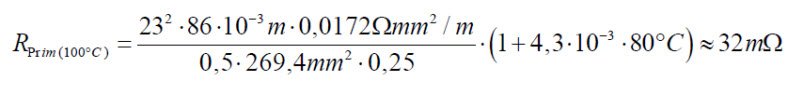
11. Calculation of the turns number of secondary (0.12).
To calculate the number of secondary turns is necessary to identify a good approximation of the real value of the voltage applied to the primary and the secondary voltage required. For this reason, is taken into account the voltage drop to the diode rectifier connected to the secondary winding, estimated at Vd = 2V, and the voltage drop to the leads of the switching element (transistor or MOSFET) estimated as VTR = 10V.
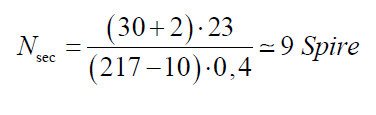
Obtaining a non-integer number of turns, it’ s approximated to the closer integer. As alternative, in an interactive way, we can recalculate the number of turns in the primary, so that the number of secondary turns is an integer number. Consider, however, that the number of turns in the primary is inversely proportional to the flux, to avoid the risk of work in the saturation zone of the core, the number of turns in the primary can be only increased.
12. Calculation of the primary current (0.14) (0.15) (0.16).
The trapezoidal current in the primary is approximated asrectangular. It’ s taken into account the magnetizing current delta Imag.
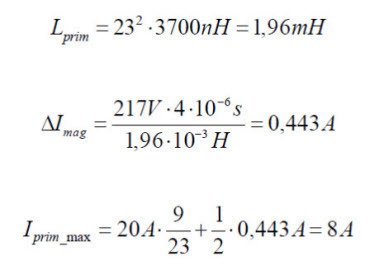
13. Calculation of the winding section (0.13).
In the forward typology we have a third winding used to demagnetize the core. The current flowing in this winding is approximately equal to the value of the magnetizing current [3]. Considering a current density of 4A/mm^2 and a magnetizing current of 0.44 A we obtain:

Let’s choose from the Table 10 in the appendix, the wire diameter 0.361 mm (AWG27). It has a surface slightly lower than that calculated, but considering also the increase of resistance for the skin effect (using a single conductor), as shown in Figure 8, of about 1%, we obtain values that are still admissible. Assuming to implement the winding of a single layer, plausible hypothesis since the number of turns of this winding is identical to the number of turns in the primary and since the length development of 23 coils doesn’ t exceed the width of the support (23 * 0.4 = 9.2 mm << 32.7mm), the section area occupied by this winding (only one layer of height approximately equal to the diameter of the conductor and width equal to the width of the substrate) we obtain:

The section of area available on the support, reduced by that necessary to achieve the winding of demagnetization will therefore be:

then for the primary winding, the estimated section size of the conductor (copper + insulation) will be:

and for the secondary:

